| Twierdzenie Talesa | |||||||||||||||
|
|||||||||||||||
| Twierdzenie Talesa – jedno z najważniejszych twierdzeń geometrii euklidesowej.Tradycja przypisuje jego sformułowanie Talesowi z Miletu.Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta. | |||||||||||||||
| Dla
powyższych rysunków zachodzi:
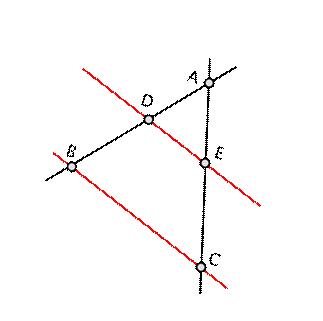
\frac{|AD|}{|AE|}=\frac{|DB|}{|EC|}=\frac{|AB|}{|AC|} lub po przekształceniu: \frac{|AE|}{|EC|}=\frac{|AD|}{|DB|} oraz \frac{|AE|}{|AC|}=\frac{|AD|}{|AB|} a także \frac{|AC|}{|EC|}=\frac{|AB|}{|DB|}. Często spotykaną nieścisłością jest takie formułowanie twierdzenia Talesa: \frac{|AD|}{|DE|}=\frac{|AB|}{|BC|}, ta równość jest oczywiście prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa. |
|||||||||||||||